위상정렬은 순서가 정해져 있는 작업을 수행할 때 차례대로 수행할 수 있도록 도와주는 정렬 알고리즘의 일종입니다.
위상정렬의 수행과정은 크게 3가지로 나눌 수 있습니다.
1. 자기 자신을 가리키는 변이 없는 꼭짓점을 찾음
2. 찾은 꼭짓점을 출력하고 출력한 꼭짓점과 그 꼭짓점에서 출발하는 변을 삭제
3. 아직 그래프에 꼭짓점이 남아있으면 단계 1로 돌아가고, 아니면 알고리즘을 종료시킨다.
-출처 위키백과
말로만 들으면 약간 어렵게 느껴질 수 있습니다. 그림과 함께 설명하겠습니다.

자기 자신을 가리키는 변이 없는 꼭짓점은 (5,7,3)으로 찾을 수 있습니다.
5를 가지고 2단계를 수행하면 5->11 이 변을 삭제하는 것입니다.
그리고 7을 가지고 2단계를 실행시키면 7->11, 7->8 두 개의 변이 삭제 됩니다.
삭제를 시키면 11이 자기 자신을 가리키는 변이 없는 꼭짓점으로 되어서 계속 이렇게 진행하게 됩니다.
꼭짓점을 다 출력하면 코드가 종료됩니다.
그림으로 보면 이해가 안 될 수도 있어서 코드와 함께 설명하겠습니다!
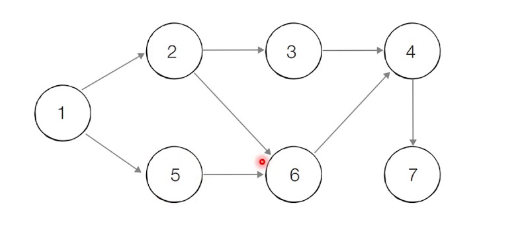
이 그림을 예시로 들어서 설명하겠습니다.
|
1
2
3
|
vertex,edge = map(int,input().split()) # 정점, 간선
in_degree = [0] * (vertex+1)
graph = [[] for _ in range(vertex+1)]
|
cs |
in_degree: 자신을 선택하고 있는 화살표의 개수를 저장하고 있는 리스트 ex) in_degree[2] -> 1
graph: 자기의 화살표가 찌르고 있는 대상들을 저장하고 있는 리스트 ex) graph[1] -> (2,5)
|
1
2
3
4
|
for _ in range(edge):
a,b = map(int,input().split())
in_degree[b] += 1
graph[a].append(b)
|
cs |
간선의 개수만큼 간선의 출발 지점과 끝 지점을 입력받고 in_degree[끝 지점] += 1, graph[시작 지점].append(끝 지점)을 해준다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
height = []
for i in range(1,(vertex+1)):
if in_degree[i] == 0:
heapq.heappush(height,i)
while height:
m = heapq.heappop(height)
print(m, end=' ')
for e in graph[m]:
in_degree[e] -= 1
if in_degree[e] == 0:
height.append(e)
|
cs |
진입차수가 0인 정점을 저장하는 height라는 리스트를 만들어준다.
1부터 정점의 개수만큼 반복하는 for 반복문을 이용해서 진입차수가 0인 정점들을 height에 넣어준다.
*위에서 in_degree[끝 지점] += 1을 해줘서 in_degree[i] == 0이면 진입 차수가 0인 정점이다.
그 후, height가 존재하면 계속 반복하는 while 반복문을 이용해서 height의 최소값을 출력하고 graph[최소값]을 이용해서 최소값에서 찌르고 있는 다른 정점들의 정보를 가져온다. 그다음 그 정점들의 in_degree값을 1 줄여준다.
*자신을 찌르고 있는 간선이 하나 줄어들기 때문에 -1을 해준다.
그리고 자신을 찌르고 있는 간선이 다 사라진 정점은 height 리스트에 추가시킨다.
여기까지 이해를 하면 위상정렬에 대해 전부 이해한 것이다.
백준에서도 위상정렬 문제를 보면 골드~플레 문제가 많은 것을 보아 위상 정렬은 코딩테스트를 위해 꼭 알아야 하는 알고리즘 같다.
읽어주셔서 감사합니다! 질문 있으시면 편하게 댓글 남겨주세요!
